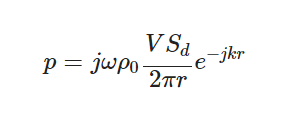音圧の式を求める
点音源についての速度ポテンシャルの式が求まりましたので、これから音圧を求めます。音圧は、速度ポテンシャルを用いると下記の式で表すことができました。
$$ p = \rho_0 \displaystyle\frac{\partial \phi}{\partial t} $$
これに式(18)を代入すると、下記となります。
$$ \begin{align} p &= \rho_0 \displaystyle\frac{\partial}{\partial t} \left( \displaystyle\frac{Q}{4 \pi r}e^{-j(kr- \omega t)} \right) \\ &= j \omega \rho_0 \displaystyle\frac{Q}{4 pi r}e^{-j(kr- \omega t)} \end{align} $$
上記の式は点音源、すなわちある一点からあらゆる方向に放射される角周波数\(\omega\)の音波において、距離\(r\)と時間\(t\)における音圧を表すものです。
しかし、スピーカーが発する音波はバッフルによって後方へは放射されず、前方にのみ放射されます。現実的には有限の面積を有するバッフルですが、ここでは理想的な無限大バッフルによって前方と後方とが完全に分断された状態を仮定します。
この場合、後方へ放射されるはずの音波はバッフルによって反射して前方に放射される音波に足し合わされると考えます。
そうすると、バッフルが無い場合の音圧に対して2倍の音圧となります。
$$ \begin{align} p &= 2 j \omega \rho_0 \displaystyle\frac{Q}{4 \pi r}e^{-j(kr- \omega t)} \\ &= j \omega \rho_0 \displaystyle\frac{Q}{2 pi r}e^{-j(kr- \omega t)} \end{align} $$
そして、体積速度\(Q\)は、振動板面積\(S_d\)と空気の粒子速度\(V\)との積で表すことができるので、上記式は下記となります。
$$ p = j \omega \rho_0 \displaystyle\frac{VS_d}{2 \pi r} e^{-j(kr- \omega t)} \tag{19} $$
式(19)は、振動板からの距離\(r\)、時間\(t\)、角周波数\(\omega\)を変数とした点音源の音圧を求める式です。
これら変数に任意の定数を代入して、時間ごとの音圧\(p\)を求めれば、正弦波の波形が得られます。
しかし、一般的にスピーカーの性能を評価するときには冒頭で紹介したように、時間\(t\)に関係なく、周波数ごとの音圧の大きさ、すなわち振幅の特性をグラフにした周波数特性で評価します。振幅の値は、\(p(t)=Ae^{j \omega t}\)における\(A\)の部分ですので、式(19)をこの形に変形しますと、下記のようになります。
$$ \begin{align} p(t) &=Ae^{j \omega t} \\ &= j \omega \rho_0 \displaystyle\frac{VS_d}{2 \pi r} e^{-jkr} \cdot e^{j \omega t} \end{align} $$
となります。
したがって、\(A\)の部分に相当する以下の部分が、音圧の振幅を求める式であり、冒頭に紹介した式(1)となります。
$$ p= j \omega \rho_0 \displaystyle\frac{VS_d}{2 \pi r} e^{-jkr} \tag{1} $$
さて、これまでスピーカーの出力音圧を求める式(1)を導出してぎしたが、実はまだ準備が足りません。式(1)の\(V\)、すなわち空気の粒子速度がわからないのです。
次は、空気の粒子速度\(V\)を求めます。