Bマトリクス
〇〇マトリクスシリーズが続きますが・・・まだ準備段階です。次はBマトリクスです。Bマトリクスとは何かというと、要素における任意の位置座標のひずみを、各節点の位置座標のひずみを元に計算するときに使う行列です。
有限要素法は、メッシュを切ることによって複数の要素に分割しますが、メッシュの切り方で要素の形状が異なります。メッシュを切るでは、三角形の要素になるようにメッシュを切りました。
要素を構成する各節点のひずみ(変位)をこれから計算で求めるわけですが、要素の内部の領域はどうなっているでしょうか。
要素内の変位
三角形要素は平面であるとします。曲面にすると滑らかになるでしょうけども、計算が複雑なので、今回は平面とします。例えば、一次元の線分を考えたときに、一方の節点を固定して(変位0)、他方の節点をy方向に1mm変位させたとしたら、線分の中間部はy方向に0.5mm変位します。
平面の三角形要素でも同様のことが言え、各節点の変位が分かれば、要素の中は計算ができてしまうということです。
今回の平面の三角形要素のように一次関数で計算することができる要素を、一次要素といいます。また、この一次関数のように、各節点と形状内部の関係を表す関数を形状関数といいます。
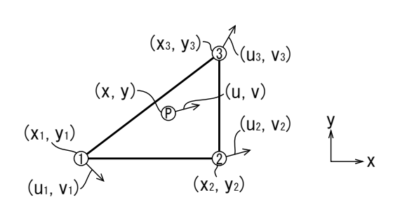
具体的には、三角形要素の各節点の座標、変位を下図のように表したとき、要素内の任意の点Pの座標と変位がどのように表すことができるかということになります。
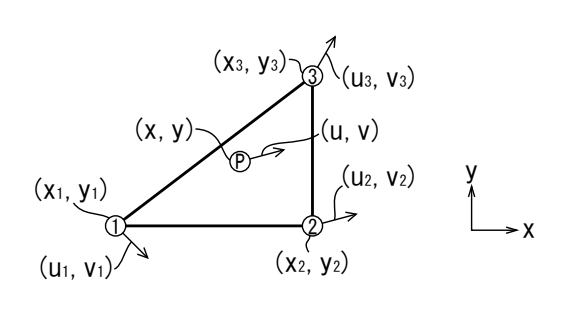
上図の節点①のx方向の変位量\(u_1\)と、節点②のx方向の変位量\(u_2\)を、x座標を用いて直線補間します。節点①と節点②の座標差\(x_2-x_1\)に対して、変位が\(u_2-u_1\)だけ変化するのですから、その変化率は\(\frac{u_2-u_1}{x_2-x_1}\)です。任意の点の位置は、\(x_1\)を基準とすると\(x-x_1\)ですから、節点①と節点②の間の稜線上にある任意の点のx方向の変位(u)は、節点①のx方向の変位(u_1)を基準とすると、
$$ \begin{align}\displaystyle\frac{u_2-u_1}{x_2-x_1}(x-x_1)+u_1&=\displaystyle\frac{u_2-u_1}{x_2-x_1}x+\displaystyle\frac{u_1x_2-u_2x_1}{x_2-x_1}\\&=Ax+B\end{align} \tag{25}$$
という一次関数の形で表すことができます。
同様に、節点①のy方向の変位量\(v_1\)と、節点②のy方向の変位量\(v_2\)を、y座標を用いて直線補間すると、節点①と節点②の間の稜線上にある任意の点のy方向の変位\(v\)は、
$$ \begin{align}\displaystyle\frac{v_2-v_1}{y_2-y_1}(y-y_1)+v_1&=\displaystyle\frac{v_2-v_1}{y_2-y_1}y+\displaystyle\frac{v_1y_2-v_2y_1}{y_2-y_1}\\&=A’y+B’\end{align}\tag{26}$$
という一次関数の形で表すことができます。
これらを重ね合わせると、三角形要素内の任意の点Pにおける変位は、
$$\begin{cases} u&=ax+by+c \\ v&=a’x+b’y+c’ \end{cases} \tag{27}$$
という一次関数で表すことができます。この\(a,b,c,a’,b’,c’\)は比例定数ですが、重ね合わせた結果どのような定数になったのか算出する必要がありますので、求めてみましょう。
上記の一次関数は、節点①~③上でも成り立ちますから、それぞれの節点について書きますと、
$$\begin{cases} u_1&=ax_1+by_1+c,\hspace{5pt}v_1=a’x_1+b’y_1+c’ \\ u_2&=ax_2+by_2+c,\hspace{5pt}v_2=a’x_2+b’y_2+c’ \\ u_3&=ax_3+by_3+c,\hspace{5pt}v_3=a’x_3+b’y_3+c’\end{cases}\tag{28} $$
となります。これを行列の形で表すと、
$$ \displaystyle\left\{ \begin{array}{c} u_1 \\ u_2 \\ u_3 \end{array} \displaystyle\right\} = \left[ \begin{array}{ccc} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{array} \right] \displaystyle\left\{ \begin{array}{c} a \\ b \\ c \end{array} \displaystyle\right\} \tag{29}$$
$$ \displaystyle\left\{ \begin{array}{c} v_1 \\ v_2 \\ v_3 \end{array} \displaystyle\right\} = \left[ \begin{array}{ccc} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{array} \right] \displaystyle\left\{ \begin{array}{c} a’ \\ b’ \\ c’ \end{array} \displaystyle\right\} \tag{30}$$
となります。
連立方程式の解法
この連立方程式を解いて、\(a,b,c,a’,b’,c’\)を求めます。もっとも、\(a,b,c\)を求めれば、同様に\(a’,b’,c’\)も求まりますので、まずは\(a,b,c\)を求めてみます。
上記の行列において、\({ u } = [X] {A}\)を変形して、\({ A } = [X]^{-1} {u}\)の形にすれば求まりますので、真ん中の行列の逆行列を求めます。
今回は、余因子を用いる方法で計算してみます。
まず、行列式\(det|X|\)を求めますと、3行3列の行列式の計算式より、
$$det|X|=x_1y_2+x_2y_3+x_3y_1-x_1y_3-x_2y_1-x_3y_2 \tag{31}$$
となります。
次に、各余因子を求めますと、
$$\begin{align} X_{11}&=(-1)^{1+1}det \left( \begin{array}{cc} y_2 & 1 \\ y_3 & 1 \end{array} \right) = y_2-y_3 \\ X_{21}&=(-1)^{2+1}det \left( \begin{array}{cc} y_1 & 1 \\ y_3 & 1 \end{array} \right) = y_3-y_1 \\ X_{31}&=(-1)^{3+1}det \left( \begin{array}{cc} y_1 & 1 \\ y_2 & 1 \end{array} \right) = y_1-y_2 \\ X_{12}&=(-1)^{1+2}det \left( \begin{array}{cc} x_2 & 1 \\ x_3 & 1 \end{array} \right) = x_3-x_2 \\ X_{22}&=(-1)^{2+2}det \left( \begin{array}{cc} x_1 & 1 \\ x_3 & 1 \end{array} \right) = x_1-x_3 \\ X_{32}&=(-1)^{3+2}det \left( \begin{array}{cc} x_1 & 1 \\ x_2 & 1 \end{array} \right) = x_2-x_1 \\ X_{13}&=(-1)^{1+3}det \left( \begin{array}{cc} x_2 & y_2 \\ x_3 & y_3 \end{array} \right) = x_2y_3-x_3y_2 \\ X_{23}&=(-1)^{2+3}det \left( \begin{array}{cc} x_1 & y_1 \\ x_3 & y_3 \end{array} \right) = x_3y_1-x_1y_3 \\ X_{33}&=(-1)^{3+3}det \left( \begin{array}{cc} x_1 & y_1 \\ x_2 & y_2 \end{array} \right) = x_1y_2-x_2y_1 \end{align} \tag{32}$$
それぞれの余因子を行列に戻すと、
$$ \begin{align} [X]^{-1}&=\displaystyle\frac{1}{det|X|} \left[ \begin{array}{ccc} X_{11} & X_{21} & X_{31} \\ X_{12} & X_{22} & X_{32} \\X_{13} & X_{23} & X_{33} \end{array} \right] \\&= \displaystyle\frac{1}{x_1y_2+x_2y_3+x_3y_1-x_1y_3-x_2y_1-x_3y_2} \left[ \begin{array}{ccc} y_2-y_3 & y_3-y_1 & y_1-y_2 \\ x_3-x_2 & x_1-x_3 & x_2-x_1 \\ x_2y_3-x_3y_2 & x_3y_1-x_1y_3 & x_1y_2-x_2y_1 \end{array} \right] \end{align} \tag{33}$$
となり、逆行列が求まりました。
ところで、上図の三角形要素の面積は、前回書いたように、
$$\Delta = \frac{1}{2} { (x_2-x_1)(y_3-y_1)-(x_3-x_1)(y_2-y_1) } \tag{34}$$
で求めることができます。これを展開すると、
$$\frac{1}{2} (x_1y_2+x_2y_3+x_3y_1-x_1y_3-x_2y_1-x_3y_2) \tag{35}$$
となり、先ほどの行列式\(det|X|\)の1/2となります。
つまり、先ほどの逆行列は、三角形の面積を\(\Delta\)で表すと、
$$ [X]^{-1}= \displaystyle\frac{1}{2\Delta} \left[ \begin{array}{ccc} y_2-y_3 & y_3-y_1 & y_1-y_2 \\ x_3-x_2 & x_1-x_3 & x_2-x_1 \\ x_2y_3-x_3y_2 & x_3y_1-x_1y_3 & x_1y_2-x_2y_1 \end{array} \right] \tag{36}$$
とまとめることができます。したがって、各比例定数は、下記のように求まります。
$$\begin{align} a&=\displaystyle\frac{1}{2\Delta} { (y_2-y_3)u_1 + (y_3-y_1)u_2 + (y_1-y_2)u_3 } \\ b&=\displaystyle\frac{1}{2\Delta} { (x_3-x_2)u_1 + (x_1-x_3)u_2 + (x_2-x_1)u_3 } \\ c&=\displaystyle\frac{1}{2\Delta} { (x_2y_3-x_3y_2)u_1 + (x_3y_1-x_1y_3)u_2 + (x_1y_2-x_2y_1)u_3 } \\ a’&=\displaystyle\frac{1}{2\Delta} { (y_2-y_3)v_1 + (y_3-y_1)v_2 + (y_1-y_2)v_3 } \\ b’&=\displaystyle\frac{1}{2\Delta} { (x_3-x_2)v_1 + (x_1-x_3)v_2 + (x_2-x_1)v_3 } \\ c’&=\displaystyle\frac{1}{2\Delta} { (x_2y_3-x_3y_2)v_1 + (x_3y_1-x_1y_3)v_2 + (x_1y_2-x_2y_1)v_3 } \end{align} \tag{37}$$
三角形要素内の任意の節点Pにおける変位は、
$$\begin{cases} u&=ax+by+c \\ v&=a’x+b’y+c’ \end{cases} \tag{27}$$
でしたから、この式に各比例定数を代入してまとめると、
$$\begin{align} u(x,y)=\displaystyle\frac{1}{2\Delta} [ { (y_2-y_3)x + (x_3-x_2)y +(x_2y_3-x_3y_2) }&u_1 \\ + { (y_3-y_1)x + (x_1-x_3)y +(x_3y_1-x_1y_3) }&u_2 \\ + { (y_1-y_2)x + (x_2-x_1)y +(x_1y_2-x_2y_1) }&u_3 ] \end{align} \tag{38}$$
$$\begin{align} v(x,y)=\displaystyle\frac{1}{2\Delta} [ { (y_2-y_3)x + (x_3-x_2)y +(x_2y_3-x_3y_2) }&v_1 \\ + { (y_3-y_1)x + (x_1-x_3)y +(x_3y_1-x_1y_3) }&v_2 \\ + { (y_1-y_2)x + (x_2-x_1)y +(x_1y_2-x_2y_1) }&v_3 ] \end{align} \tag{39}$$
と求まります。
このままだと見にくいので、変数である変位\(u_n,v_n\)以外の部分を形状関数\(N_n\)としてまとめます。
$$\begin{cases} N_1(x,y)=\displaystyle\frac{1}{2\Delta} { (y_2-y_3)x + (x_3-x_2)y +(x_2y_3-x_3y_2) } \\ N_2(x,y)=\displaystyle\frac{1}{2\Delta} { (y_3-y_1)x + (x_1-x_3)y +(x_3y_1-x_1y_3) } \\ N_3(x,y)=\displaystyle\frac{1}{2\Delta} { (y_1-y_2)x + (x_2-x_1)y +(x_1y_2-x_2y_1) } \end{cases} \tag{40}$$
すると、三角形要素内の任意の節点Pにおける変位は、
$$\begin{cases} u&=N_1u_1+N_2u_2+N_3u_3 \\ v&=N_1v_1+N_2v_2+N_3v_3 \end{cases} \tag{41} $$
と簡単な式にまとまります。結局のところ、形状関数\(N_n\)は、各節点における変位\(u_n,v_n\)に対して、重み付けをしていることになりますね。
ひずみの導出
さて、三角形要素の任意の座標における変位を、各節点と関連づける式が求まったところで、ひずみを求めてみます。
ひずみは、変位を元の形状で微分したものですから、上記で求まった式を、各方向別にその座標で偏微分することになります。
$$\begin{cases} \displaystyle\frac{\partial u}{\partial x}=\displaystyle\frac{\partial N_1}{\partial x}u_1+\displaystyle\frac{\partial N_2}{\partial x}u_2+\displaystyle\frac{\partial N_3}{\partial x}u_3 \\ \displaystyle\frac{\partial u}{\partial y}=\displaystyle\frac{\partial N_1}{\partial y}u_1+\displaystyle\frac{\partial N_2}{\partial y}u_2+\displaystyle\frac{\partial N_3}{\partial y}u_3 \\ \displaystyle\frac{\partial v}{\partial x}=\displaystyle\frac{\partial N_1}{\partial x}v_1+\displaystyle\frac{\partial N_2}{\partial x}v_2+\displaystyle\frac{\partial N_3}{\partial x}v_3 \\ \displaystyle\frac{\partial v}{\partial y}=\displaystyle\frac{\partial N_1}{\partial y}v_1+\displaystyle\frac{\partial N_2}{\partial y}v_2+\displaystyle\frac{\partial N_3}{\partial y}v_3 \end{cases} \tag{42}$$
ところで、Dマトリクスの記事では、ひずみと応力は6つあると書きました。
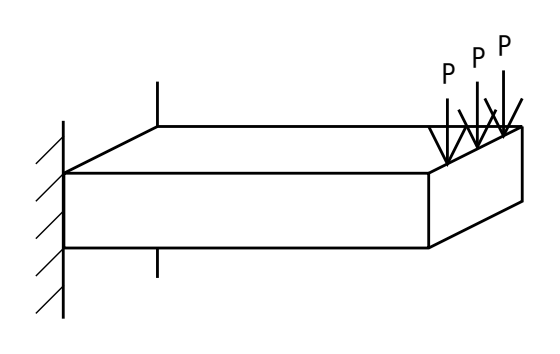
しかし、今回解析しようとしているような片持ち梁は、奥行方向は千歳飴のように同じ断面形状が連続していると考えることで、平面のひずみの状態が奥行方向にも同様に広がっているとみなすことができます。このようなモデルを平面ひずみモデルと呼びます。
平面ひずみモデルにおけるxy平面の2次元ひずみは、
$$ { \varepsilon } = \displaystyle\left\{ \begin{array}{c} \varepsilon_x \\ \varepsilon_y \\ \gamma_{xy} \end{array} \displaystyle\right\} \tag{43}$$
の3つの成分のみに省略できます。そうなると、各ひずみは、
$$ { \varepsilon } = \displaystyle\left\{ \begin{array}{c} \displaystyle\frac{\partial u}{\partial x} \\ \displaystyle\frac{\partial v}{\partial y} \\ \displaystyle\frac{\partial u}{\partial y}+\displaystyle\frac{\partial v}{\partial x} \end{array} \displaystyle\right\} \tag{44}$$
のように表すことができます。
これに、形状関数を用いた式を代入して、
$$ { \varepsilon } = \displaystyle\left\{ \begin{array}{l} \displaystyle\frac{\partial N_1}{\partial x}u_1+\displaystyle\frac{\partial N_2}{\partial x}u_2+\displaystyle\frac{\partial N_3}{\partial x}u_3 \\ \displaystyle\frac{\partial N_1}{\partial y}v_1+\displaystyle\frac{\partial N_2}{\partial y}v_2+\displaystyle\frac{\partial N_3}{\partial y}v_3 \\ \displaystyle\frac{\partial N_1}{\partial y}u_1+\displaystyle\frac{\partial N_2}{\partial y}u_2+\displaystyle\frac{\partial N_3}{\partial y}u_3+\displaystyle\frac{\partial N_1}{\partial x}v_1+\displaystyle\frac{\partial N_2}{\partial x}v_2+\displaystyle\frac{\partial N_3}{\partial x}v_3 \end{array} \displaystyle\right\} \tag{45}$$
となります。これを行列で表すと、
$$ \begin{align} { \varepsilon } &= \left[ \begin{array}{cccccc} \displaystyle\frac{\partial N_1}{\partial x} & 0 & \displaystyle\frac{\partial N_2}{\partial x} & 0 & \displaystyle\frac{\partial N_3}{\partial x} & 0 \\ 0 & \displaystyle\frac{\partial N_1}{\partial y} & 0 & \displaystyle\frac{\partial N_2}{\partial y} & 0 & \displaystyle\frac{\partial N_3}{\partial y} \\ \displaystyle\frac{\partial N_1}{\partial y} & \displaystyle\frac{\partial N_1}{\partial x} & \displaystyle\frac{\partial N_2}{\partial y} & \displaystyle\frac{\partial N_2}{\partial x} & \displaystyle\frac{\partial N_3}{\partial y} & \displaystyle\frac{\partial N_3}{\partial x} \end{array} \right] \displaystyle\left\{ \begin{array}{c} u_1 \\ v_1 \\ u_2 \\ v_2 \\ u_3 \\ v_3 \end{array} \displaystyle\right\} \\ &= \displaystyle\frac{1}{2\Delta} \left[ \begin{array}{cccccc} y2-y_3 & 0 & y_3-y_1 & 0 & y_1-y_2 & 0 \\ 0 & x_3-x_2 & 0 & x_1-x_3 & 0 & x_2-x_1 \\ x_3-x_2 & y_2-y_3 & x_1-x_3 & y_3-y_1 & x_2-x_1 & y_1-y_2 \end{array} \right] \displaystyle\left\{ \begin{array}{c} u_1 \\ v_1 \\ u_2 \\ v_2 \\ u_3 \\ v_3 \end{array} \displaystyle\right\} \end{align} \tag{46}$$
この、真ん中の行列を取り出してまとめますと、
$$ \begin{align} [ B ] &= \left[ \begin{array}{cccccc} \displaystyle\frac{\partial N_1}{\partial x} & 0 & \displaystyle\frac{\partial N_2}{\partial x} & 0 & \displaystyle\frac{\partial N_3}{\partial x} & 0 \\ 0 & \displaystyle\frac{\partial N_1}{\partial y} & 0 & \displaystyle\frac{\partial N_2}{\partial y} & 0 & \displaystyle\frac{\partial N_3}{\partial y} \\ \displaystyle\frac{\partial N_1}{\partial y} & \displaystyle\frac{\partial N_1}{\partial x} & \displaystyle\frac{\partial N_2}{\partial y} & \displaystyle\frac{\partial N_2}{\partial x} & \displaystyle\frac{\partial N_3}{\partial y} & \displaystyle\frac{\partial N_3}{\partial x} \end{array} \right] \\ &= \displaystyle\frac{1}{2\Delta} \left[ \begin{array}{cccccc} y2-y_3 & 0 & y_3-y_1 & 0 & y_1-y_2 & 0 \\ 0 & x_3-x_2 & 0 & x_1-x_3 & 0 & x_2-x_1 \\ x_3-x_2 & y_2-y_3 & x_1-x_3 & y_3-y_1 & x_2-x_1 & y_1-y_2 \end{array} \right] \end{align} \tag{47}$$
となります。この\([ B ] \)を、Bマトリクスといいます。やっと出てきたBマトリクス!!
最終的に、ひずみと変位との関係は、Bマトリクスを用いて
$$ { \varepsilon } = [ B ] { u } \tag{48}$$
と表すことができます。
このBマトリクスは三角形一次要素のBマトリクスです。Bマトリクスは要素の形状によって決まるため、四角形要素や二次要素では中身が変わります。