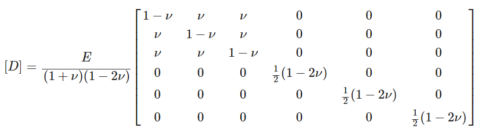Dマトリクス
さて、応力テンソルについて頭に入ったところで、次にひずみの関係式を応力テンソルを使って表します。このときに使うのがDマトリクスという行列です。
引っ張りによるひずみ
まず、引っ張りによるひずみを考えます。
ヤング率\(E\)の材料にx方向に引っ張り応力\(\sigma_x\)が生じたときのx方向のひずみ\(\varepsilon_x\)は、フックの法則から、
$$ \varepsilon_x = \displaystyle\frac{\sigma_x}{E} \tag{11} $$
と表すことができます。このとき、x方向は伸びますが、y方向には縮むという現象が生じます。同様に、z方向に伸びたときにも、y方向は縮みます。このときの縮み量は、ポアソン比\(\nu\)を使って、
$$ \varepsilon_y = – \nu ( \varepsilon_x+\varepsilon_z) = – \nu \displaystyle\frac{\sigma_x+\sigma_z}{E} \tag{12} $$
と表すことができます。
つまり、x方向のひずみは、引っ張り応力による伸びと、y方向及びz方向の引っ張り応力による縮みの差で表すことができ、
$$ \varepsilon_x = \displaystyle\frac{1}{E} { \sigma_x – \nu ( \sigma_y+\sigma_z) } \tag{13} $$
となります。同様に、y方向、z方向は、
$$ \begin{align} \varepsilon_y &= \displaystyle\frac{1}{E} { \sigma_y – \nu ( \sigma_x+\sigma_z) } \\ \varepsilon_z &= \displaystyle\frac{1}{E} { \sigma_z – \nu ( \sigma_x+\sigma_y) } \end{align} \tag{14} $$
となります。
せん断によるひずみ
次に、せん断によるひずみを考えます。
横弾性係数\(G\)の材料にせん断応力\(\tau_{xy}\)が生じたときのy方向のひずみ\(\gamma_{xy}\)は、引っ張り応力\(\sigma_n\)には無関係で、
$$ \gamma_{xy}=\displaystyle\frac{\tau_{xy}}{G} \tag{15} $$
で表すことができます。
横弾性係数\(G\)は、ヤング率\(E\)との関係で下記のように表すことができます。
$$G=\displaystyle\frac{E}{2(1+\nu)} \tag{16} $$
これを踏まえて、x,y,z各方向についてのせん断ひずみを求めると、
$$ \begin{align} \gamma_{xy} &= \displaystyle\frac{E}{2(1+\nu)} \tau_{xy} \\ \gamma_{yz} &= \displaystyle\frac{E}{2(1+\nu)} \tau_{yz} \\ \gamma_{zx} &= \displaystyle\frac{E}{2(1+\nu)} \tau_{zx} \end{align} \tag{17} $$
となります。
これらより、各ひずみと各応力との関係をまとめると、
$$ \displaystyle\left\{ \begin{array}{c} \varepsilon_x \\ \varepsilon_y \\ \varepsilon_z \\ \gamma_{xy} \\ \gamma_{yz} \\ \gamma_{zx} \end{array} \displaystyle\right\} = \displaystyle\frac{1}{E} \left[ \begin{array}{cccccc} 1 & – \nu & – \nu & 0 & 0 & 0 \\ – \nu & 1 & – \nu & 0 & 0 & 0 \\ – \nu & – \nu & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 2 ( 1+ \nu) & 0 & 0 \\ 0 & 0 & 0 & 0 & 2 ( 1+ \nu) & 0\\ 0 & 0 & 0 & 0 & 0 & 2 ( 1+ \nu) \\ \end{array} \right] \displaystyle\left\{ \begin{array}{c} \sigma_x \\ \sigma_y \\ \sigma_z \\ \tau_{xy} \\ \tau_{yz} \\ \tau_{zx} \end{array} \displaystyle\right\} \tag{18} $$
となります。
逆行列を求める
この行列は\(\varepsilon = \frac{1}{E} \sigma\)の形をしていることが分かります。これを変形して、\( \sigma = E \varepsilon\)の形にします。
この場合、真ん中の6行6列の行列の逆行列を求める必要があります。逆行列の求め方はいくつかありますが、ここではガウスの消去法を使って\((A I)\)を\((I B)\)に変形して逆行列\(B=A^{-1}\)とする方法で求めてみます。
ここで、真ん中の6行6列の行列は、左上3行3列の行列と、右下の3行3列の行列と、右上及び左下の零行列の4つの行列からなるブロック行列とみることが出来ます。そこで、左上3行3列の行列と、右下の3行3列の行列を別々に計算します。
まず、左上3行3列の行列です。係数の\(\frac{1}{E}\)は取り出しておいて、行列の中身に基本変形を加えます。最初に前進消去です。1行目に\(\nu\)を乗じて2行目と3行目に足します。
$$ \left[ \begin{array}{cccccc} 1 & – \nu & – \nu &1&0&0 \\ – \nu & 1 & – \nu &0&1&0\\ – \nu & – \nu & 1 &0&0&1\end{array} \right] =\left[ \begin{array}{cccccc} 1 & – \nu & – \nu &1&0&0\\ 0 & 1-\nu^2 & – \nu(1+\nu) &\nu&1&0\\ 0 &- \nu(1+\nu) & 1-\nu^2 & \nu &0&1\end{array} \right]$$
2行目に\(\frac{1}{1-\nu^2}\)を乗じます。
$$ \left[ \begin{array}{cccccc} 1 & – \nu & – \nu &1&0&0\\ 0 & 1 & – \displaystyle\frac{\nu}{1-\nu} & \displaystyle\frac{\nu}{1-\nu^2}&- \displaystyle\frac{1}{1-\nu^2}&0\\ 0 &- \nu(1+\nu) & 1-\nu^2 & \nu &0&1\end{array} \right]$$
2行目に\(\nu(1+\nu)\)を乗じたものを3行目に足します。
ついでに、2行目に\(\nu\)を乗じたものを1行目に足します。これは本当は後進代入の操作なのですが、めんどくさいのでこのタイミングでやっておきます。
$$ \left[ \begin{array}{cccccc} 1&0& – \displaystyle\frac{\nu}{1-\nu} &- \displaystyle\frac{1}{1-\nu^2}&- \displaystyle\frac{\nu}{1-\nu^2}&0\\ 0&1& – \displaystyle\frac{\nu}{1-\nu} & \displaystyle\frac{\nu}{1-\nu^2}&- \displaystyle\frac{1}{1-\nu^2}&0\\ 0&0& \displaystyle\frac{(1+\nu)(1-2\nu)}{1-\nu} & \displaystyle\frac{\nu}{1-\nu}&\displaystyle\frac{\nu}{1-\nu}&1\end{array} \right]$$
3行目に\(\frac{1-\nu}{(1+\nu)(1-2\nu)}\)を乗じます。
$$ \left[ \begin{array}{cccccc} 1&0& – \displaystyle\frac{\nu}{1-\nu} &- \displaystyle\frac{1}{1-\nu^2}&- \displaystyle\frac{\nu}{1-\nu^2}&0\\ 0&1& – \displaystyle\frac{\nu}{1-\nu} & \displaystyle\frac{\nu}{1-\nu^2}&- \displaystyle\frac{1}{1-\nu^2}&0\\ 0&0&1& \displaystyle\frac{\nu}{(1+\nu)(1-2\nu)}&\displaystyle\frac{\nu}{(1+\nu)(1-2\nu)}&\displaystyle\frac{1-\nu}{(1+\nu)(1-2\nu)}\end{array} \right]$$
これで前進消去が終わりましたので、次に後進代入します。といっても1ステップで終わりです。3行目に\(\frac{\nu}{1-\nu}\)を乗じたものを1行目と2行目に足します。
$$ \left[ \begin{array}{cccccc} 1&0&0&\displaystyle\frac{1-\nu}{(1+\nu)(1-2\nu)}&\displaystyle\frac{\nu}{(1+\nu)(1-2\nu)}&\displaystyle\frac{\nu}{(1+\nu)(1-2\nu)}\\ 0&1&0& \displaystyle\frac{\nu}{(1+\nu)(1-2\nu)}&\displaystyle\frac{1-\nu}{(1+\nu)(1-2\nu)}&\displaystyle\frac{\nu}{(1+\nu)(1-2\nu)}\\ 0&0&1& \displaystyle\frac{\nu}{(1+\nu)(1-2\nu)}&\displaystyle\frac{\nu}{(1+\nu)(1-2\nu)}&\displaystyle\frac{1-\nu}{(1+\nu)(1-2\nu)}\end{array} \right] \tag{19} $$
これで\((I B)\)の形になりました。共通項をまとめて係数\(E\)に乗じて前に出すと、左上の行列の逆行列は、
$$ \displaystyle\frac{E}{(1+\nu)(1-2\nu)}\left[ \begin{array}{ccc} 1-\nu&\nu&\nu\\ \nu&1-\nu&\nu\\ \nu&\nu&1-\nu \end{array} \right] \tag{20} $$
となります。
さて、もう一方の右下の行列の逆行列ですが、こちらもガウスの消去法を使います。しかし、こちらはとても単純で、全部の行に\(\frac{1}{2(1+\nu)}\)を乗じれば完了です。
$$ \left[ \begin{array}{cccccc} 2(1+\nu) &0&0&1&0&0\\ 0& 2(1+\nu) &0&0&1&0\\ 0&0& 2(1+\nu) &0&0&1\end{array} \right]=\left[ \begin{array}{cccccc} 1&0&0&\displaystyle\frac{1}{2(1+\nu)}&0&0\\ 0&1&0&0&\displaystyle\frac{1}{2(1+\nu)}&0\\ 0&0&1&0&0&\displaystyle\frac{1}{2(1+\nu)} \end{array} \right] $$
ここでも共通項を係数として前に出しますが、先程の左上の行列の係数と揃えるためにちょっと細工しますと、
$$ \displaystyle\frac{E}{(1+\nu)(1-2\nu)}\left[ \begin{array}{ccc} \frac{1}{2}(1-2\nu)&0&0 \\0&\frac{1}{2}(1-2\nu)&0\\ 0&0&\frac{1}{2}(1-2\nu) \end{array} \right] \tag{21} $$
となります。
これらの逆行列をもとのブロック行列に戻すと、
$$ \displaystyle\frac{E}{(1+\nu)(1-2\nu)}\left[ \begin{array}{cccccc} 1-\nu&\nu&\nu&0&0&0\\ \nu&1-\nu&\nu&0&0&0\\ \nu&\nu&1-\nu &0&0&0\\ 0&0&0&\frac{1}{2}(1-2\nu)&0&0 \\ 0&0&0&0&\frac{1}{2}(1-2\nu)&0 \\ 0&0&0&0&0&\frac{1}{2}(1-2\nu) \end{array} \right] \tag{22} $$
となります。これで、もとの行列の逆行列が求まりました。
フックの法則の形へ変形
したがって、応力ベクトルを求める式は、
$$ \displaystyle\left\{ \begin{array}{c} \sigma_x \\ \sigma_y \\ \sigma_z \\ \tau_{xy} \\ \tau_{yz} \\ \tau_{zx} \end{array} \displaystyle\right\} = \displaystyle\frac{E}{(1+\nu)(1-2\nu)} \left[ \begin{array}{cccccc} 1-\nu & \nu & \\nu & 0 & 0 & 0 \\ \nu & 1-\nu & \nu & 0 & 0 & 0 \\ \nu & \nu & 1-\nu & 0 & 0 & 0 \\ 0 & 0 & 0 & \frac{1}{2} ( 1-2 \nu) & 0 & 0 \\ 0 & 0 & 0 & 0 & \frac{1}{2} ( 1-2 \nu) & 0\\ 0 & 0 & 0 & 0 & 0 & \frac{1}{2} ( 1-2 \nu) \\ \end{array} \right] \displaystyle\left\{ \begin{array}{c} \varepsilon_x \\ \varepsilon_y \\ \varepsilon_z \\ \gamma_{xy} \\ \gamma_{yz} \\ \gamma_{zx} \end{array} \displaystyle\right\} \tag{23} $$
となります。
この真ん中の行列を取り出して、
$$ [ D ] = \displaystyle\frac{E}{(1+\nu)(1-2\nu)} \left[ \begin{array}{cccccc} 1-\nu & \nu & \nu & 0 & 0 & 0 \\ \nu & 1-\nu & \nu & 0 & 0 & 0 \\ \nu & \nu & 1-\nu & 0 & 0 & 0 \\ 0 & 0 & 0 & \frac{1}{2} ( 1-2 \nu) & 0 & 0 \\ 0 & 0 & 0 & 0 & \frac{1}{2} ( 1-2 \nu) & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{1}{2} ( 1-2 \nu) \end{array} \right] $$
とおくと、先ほどの式は、
$$ \{ \sigma \} = [ D ] \{ \varepsilon \} \tag{24} $$
と表すことができます。
この\( [ D ] \)をDマトリクスといいます。Dマトリクスは、材料の特性を表すマトリクスです。
結局何をしていたかというと、一軸のスカラーにおけるヤング率の考え方を、一般的な3次元の場合に拡張して、応力テンソルの場合のヤング率とでも言うべき行列を求めたということですね。