はじめに
構造設計の仕事をしていると、「なんとなく」従来の設計を踏襲したパラメータを適用して設計しがちです。または、「なんとなく」常識的にこのくらいの寸法が妥当かなという感じで設計していることもあると思います。
ところが、最低限の肉厚がどのくらい必要かとか、壊れないギリギリのところでできるだけ軽くしようとか、こういった目標がはっきりしている設計をするときに、「なんとなく」設計するとうまくいきません。それで、「とりあえず」試作して確認してみようという発想になります。
こういった「なんとなく設計」「とりあえず試作」では、「それなり」の製品しかできませんので、設計者としても将来が心配です。
そこで、ちゃんと設計計算しようということになるわけですが、今は本当にいい時代で、有限要素法の強度解析ならば使いやすいUIのフリーソフトもたくさんあります。でも、オペレーションはすぐにできても、出てきた結果が評価できないとか、その結果は信頼できるのか、という話になると自信のない人も多いと思います。
この記事では、有限要素法の強度解析の手順を、EXCELを用いて解説してみようと思います。
解析のモデルは、定番の「先端に集中荷重を受ける片持ち梁」です。モデル化するとこんな感じです。ちなみに、単純にするために2次元で考えます。
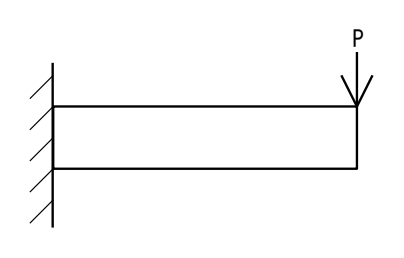
実際に設計していて、このような構造になる製品は少ないような気はしますが、理解のためにはシンプルなので、これを用います。
メッシュを切る
まず、梁を複数の要素に分割します。これを離散化するとか、メッシュを切るとか言います。
どのくらい細かく分割するかは計算精度に影響したりするんですが、今回は勉強のために下図のようにかなり粗めに分割します。
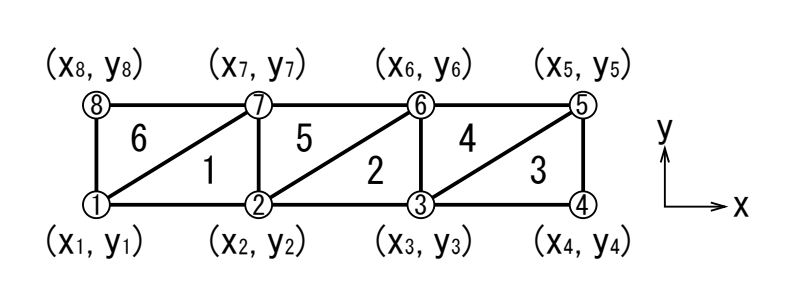
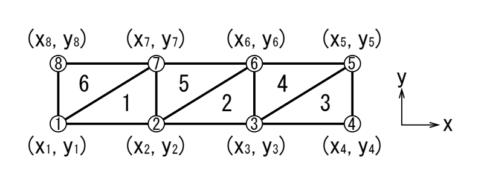
①~⑧は節点とかノードといいます。今回は8個の節点に分割しています。\(x_n,y_n\)は各節点のx座標とy座標です。つまり寸法のことですね。
1~6は3つの節点で囲まれた部分で、要素とかエレメントといいます。8個の節点で三角形の要素を構成しているので、要素の数は6個となります。
要素の番号の振り方はどこかを基準として反時計回りにする習慣にするとよいです。要素の形は三角形や四角形がありますが、今回は単純に計算できるので三角形を選びました。
また、三角形要素ですので、各節点の座標を用いると、各要素の面積を求めることができます。任意の3つの座標点における面積の公式を利用して求めることができますが、今回は等間隔の節点で分割しているので、各要素の面積は6つとも同じになります。
各要素を構成している節点のグループごとにまとめると、下表のようになります。
| 要素番号 | 節点番号 | x座標 | y座標 | 面積 |
|---|---|---|---|---|
| 1 | ① | \(x_1\) | \(y_1\) | \(\Delta=\displaystyle\frac{1}{2} \displaystyle\{ (x_2-x_1)(y_7-y_1)-(x_7-x_1)(y_2-y_1) \displaystyle\} \) |
| ② | \(x_2\) | \(y_2\) | ||
| ⑦ | \(x_7\) | \(y_7\) | ||
| 2 | ② | \(x_2\) | \(y_2\) | \(\Delta = \displaystyle\frac{1}{2} \displaystyle\{ (x_3-x_2)(y_6-y_2)-(x_6-x_2)(y_3-y_2) \displaystyle\} \) |
| ③ | \(x_3\) | \(y_3\) | ||
| ⑥ | \(x_6\) | \(y_6\) | ||
| 3 | ③ | \(x_3\) | \(y_3\) | \(\Delta = \displaystyle\frac{1}{2} \displaystyle\{ (x_4-x_3)(y_5-y_3)-(x_5-x_3)(y_4-y_3) \displaystyle\} \) |
| ④ | \(x_4\) | \(y_4\) | ||
| ⑤ | \(x_5\) | \(y_5\) | ||
| 4 | ③ | \(x_3\) | \(y_3\) | \(\Delta = \displaystyle\frac{1}{2} \displaystyle\{ (x_5-x_3)(y_6-y_3)-(x_6-x_3)(y_5-y_3) \displaystyle\} \) |
| ⑤ | \(x_5\) | \(y_5\) | ||
| ⑥ | \(x_6\) | \(y_6\) | ||
| 5 | ② | \(x_2\) | \(y_2\) | \(\Delta = \displaystyle\frac{1}{2} \displaystyle\{ (x_6-x_2)(y_7-y_2)-(x_7-x_2)(y_6-y_2) \displaystyle\} \) |
| ⑥ | \(x_6\) | \(y_6\) | ||
| ⑦ | \(x_7\) | \(y_7\) | ||
| 6 | ① | \(x_1\) | \(y_1\) | \(\Delta =\displaystyle\frac{1}{2} \displaystyle\{ (x_7-x_1)(y_8-y_1)-(x_8-x_1)(y_7-y_1) \displaystyle\} \) |
| ⑦ | \(x_7\) | \(y_7\) | ||
| ⑧ | \(x_8\) | \(y_8\) |
有限要素法では、本来連続体であるモデルを、上記のように有限個の要素に分割して計算していくことになります。次に、要素ごとに剛性マトリクスというものを求めます。